평면 위에 존재하는 점 하나가 있고
특정 거리를 이동한 곳에 또 점 하나를 찍었습니다.
이러한 점을 여러 개 찍고 이 점들이 모이면

하나의 '원'을 구성하게 됩니다.
중심에 존재하는 점과 원을 이루는 점들과의
거리는 모두 같을 겁니다.
이 길이를 반지름(radius, r)이라고 하죠.
지름을 수식으로 나타내면
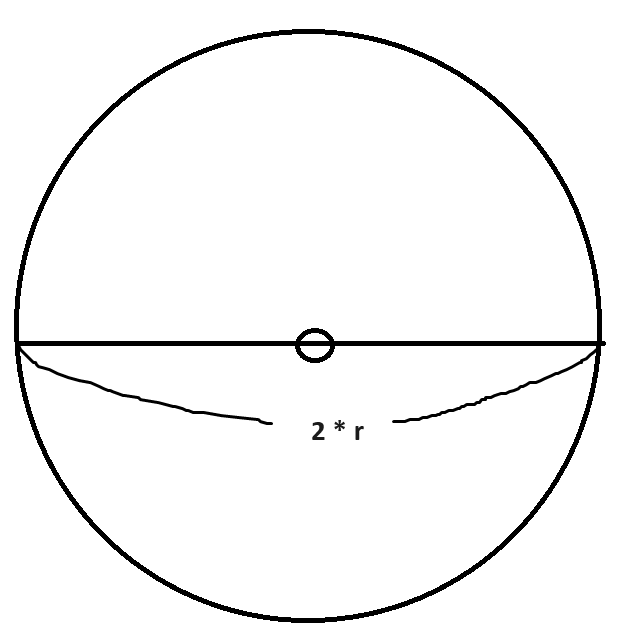
반지름의 두 배이므로
2 * r 로 표현할 수 있습니다.
그럼 위와 같은 원의 둘레는 어떻게 구할까요?
반지름만 알고 있다면 원의 둘레는 쉽게 구할 수 있습니다.
바로 원주율을 이용하면 되는데요,
원의 둘레( 원주 )는 지름 길이에
파이( π, 3.14159265359... )를
곱하면 나옵니다.
수식으로 나타내면
원의 둘레 = 2 * r * π 인 것이죠.
근데 왜 지름에 파이를 곱하면
원의 둘레를 알 수 있는 것일까요?
원의 둘레와 지름에 대한 비율이
파이( π, 3.14159265359... )이기 때문입니다.
원의 지름이 4cm라면 3.14를 곱해
원의 둘레가 12.56cm임을 알 수 있고,
원의 지름이 14cm라면 3.14를 곱해
원의 둘레가 43.96cm임을 알 수 있죠.
그렇다면
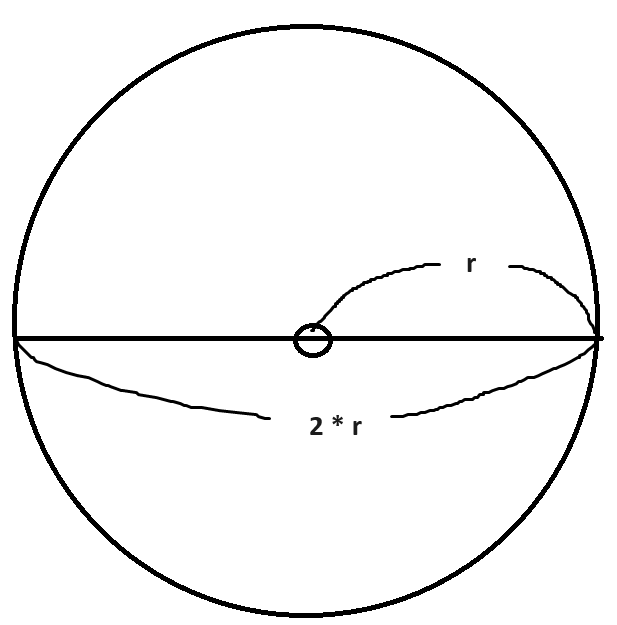
지름에 π를 곱하는 것이 아닌
반지름에 π를 곱하면 무엇을 얻을 수 있을까요?
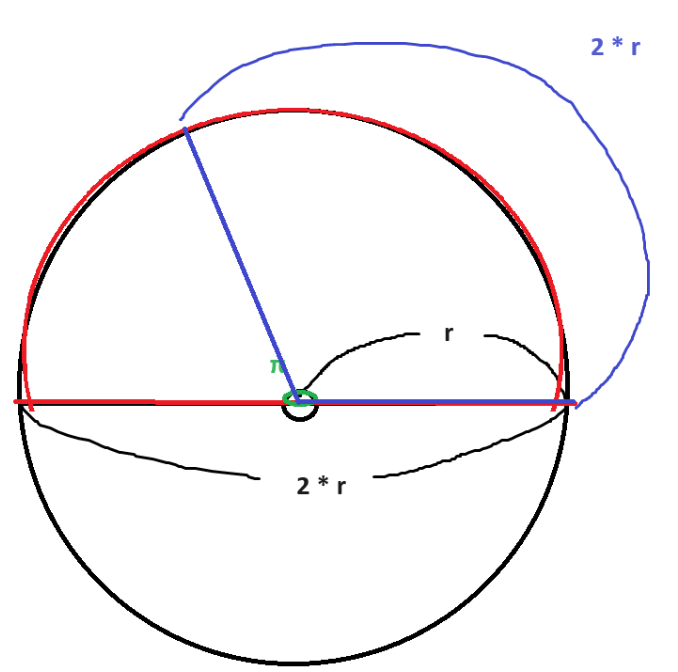
아래 그림에서 빨간 부분과 같은,
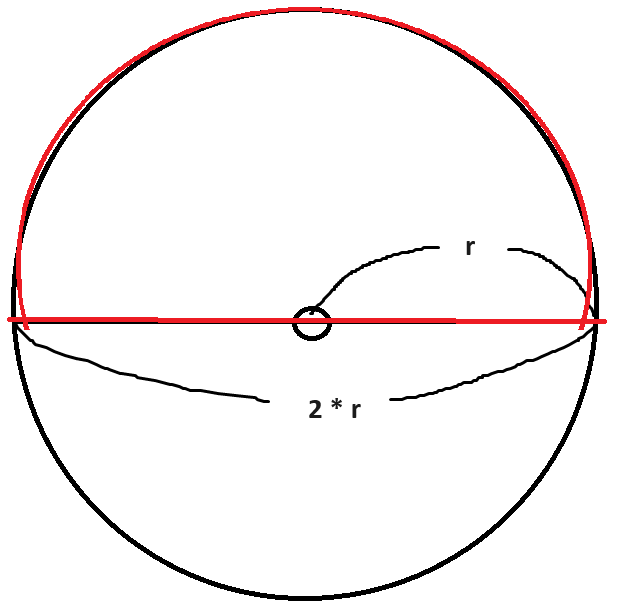
즉 원의 전체 둘레가 아닌
원에서 절반 부분에 해당하는
둘레의 길이를 알 수 있겠죠.
결국 파이라는 것은 전체 각도의
절반을 의미하게 되는 겁니다.

왜냐하면 반지름에 파이를 곱하면
원의 전체 둘레 중 절반에 해당하므로
이를 전체 한 바퀴 중 반 바퀴로 보겠다는 거죠.
이처럼 원의 둘레와 반지름 사이의 비율을
곧 각도로 보고 있는 게 바로 라디안( radian )이라는
각도입니다.
더 자세히 파고들어 봅시다.
3.14 radian이 원의 전체 둘레의 절반에
해당하는 각도, 즉 60분법으로 표현하면 180도이죠.
그렇다면 1 radian은 무엇을 의미할까요?
3.14 라디안이 180도니까,
1 라디안은 대략 57도 정도네요.
하지만 이러한 각도가 중요한 것이 아닙니다.

1 라디안이라는 것은
원의 절반에 해당하는 부분을 기준으로
호의 길이와 반지름이 1:1 비율을
완성시키는 지점의 각도인 거죠.
즉 호의 길이와 반지름의 길이가 같으려면
1 라디안의 각도가 필요한 것이며,
1 라디안( 57도 ) 정도가 호의 길이와 반지름의
길이가 같아지는 지점이라는 것이죠.
그럼 2 라디안은
60분법으로 표현하면 대략 114도이며
원의 절반에 해당하는 부분을 기준으로
호의 길이와 반지름이 2:1 비율을
완성시키는 지점의 각도인 거죠.
즉 2 라디안( 114도) 정도가
호의 길이가 반지름 길이의 2배가 되는 지점인 것이죠.
이제 라디안과 삼각함수를 접목시킬 건데,
먼저 삼각함수에 대해 알아봅시다.
삼각함수의 종류로는
sinθ(사인), cosθ(코사인), tanθ(탄젠트)가 있으며
이것은 직각삼각형에 적용하게 됩니다.
( θ는 임의의 각으로 여기서는 라디안을 의미합니다. )
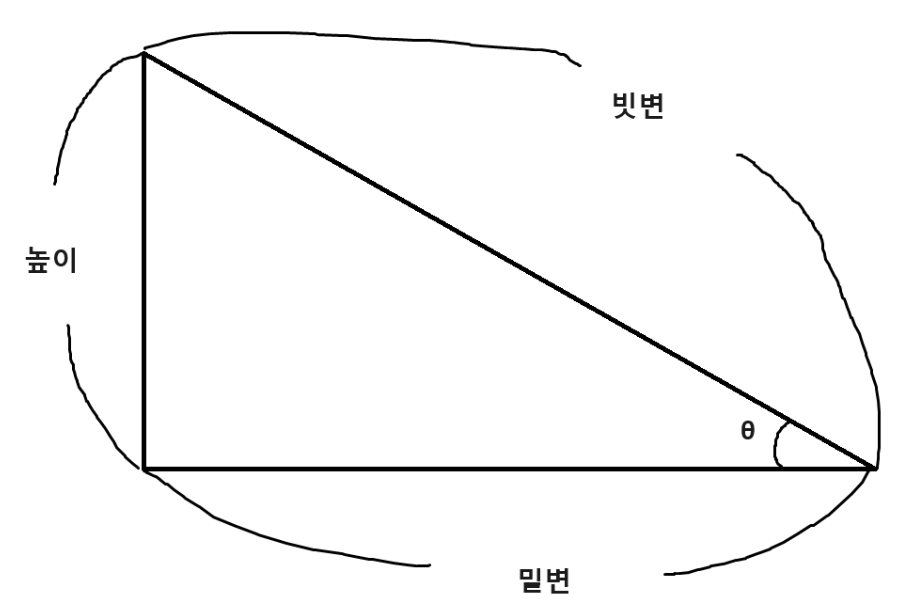
sinθ는 높이 / 빗변으로 높이를 빗변으로 나누어
빗변과 높이와의 비율을 파악하고자 하는 것이죠.
cosθ는 밑변 / 빗변으로 밑변을 빗변으로 나누어
빗변과 밑변과의 비율을 파악하고자 하는 것이죠.
tanθ는 높이 / 밑변으로 높이를 밑변으로 나누어
밑변과 높이와의 비율을 파악하고자 하는 것이죠.
아래 삼각형을 삼각함수 cosθ를 통해

비율을 파악해 봤더니 빗변이 1이고 밑변이 0.5였다고 합시다.
그럼 만약 빗변의 길이가 100이면 밑변의 길이는 절반인 50일 겁니다.
이처럼 이 비율을 알고 있다면 빗변의 길이만
알고 있어도 밑변의 길이를 파악할 수 있게 되는 거죠.
이번에도 비율을 파악해 봤더니
빗변이 1이고 밑변이 0.5였다고 합시다.
이때 빗변의 길이가 1이라고 가정합시다.
이 경우에는 결국 cosθ의 값 자체가 밑변의 길이가 되겠죠.
왜냐하면 cosθ는 밑변 / 빗변, 즉 0.5 / 1 이 되니까요.
여기서 알 수 있는 것은
cosθ는 비율을 나타내는 것이지만,
기준이 되는 빗변의 실제 길이가 1이 되면
비율의 값 자체가 밑변의 길이가 되어 버리는 것입니다.
이를 이용해 아래 그림처럼
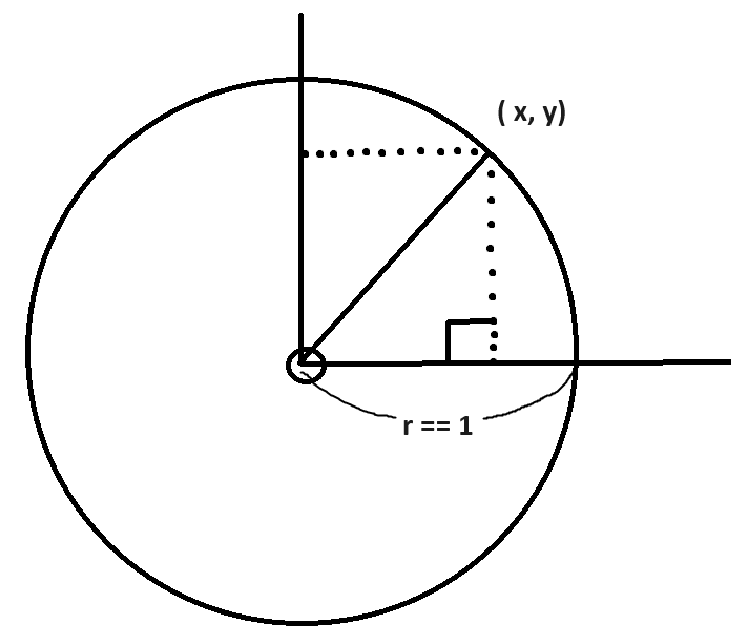
원의 반지름이 1이라면
x와 y 좌푯값을 구할 수 있습니다.
x 좌푯값은 밑변의 길이와 같을 것이고,
y 좌푯값은 높이의 길이와 같을 겁니다.
원의 반지름이 1이므로
빗변의 길이는 1인 것이 확정이죠.
이 상태에서 cosθ를 통해
밑변 / 빗변의 비율을 나타내죠?
이때 빗변의 길이는 1이고 밑변의 길이는
알 수 없어 비율로 나타낼 수 없습니다.
비율을 나타낼 수 없기 때문에
밑변의 길이도 구할 수 없을 것 같지만
사실 빗변의 길이가 1이므로
결국 cosθ의 비율 값 자체가 밑변의
길이죠. 즉 x 좌푯값은 cosθ입니다.
마찬가지로 sinθ를 통해 높이 / 빗변의
비율을 나타낼 수 있고, 빗변의 길이가 1이므로
높이는 결국 sinθ의 비율 값 자체가 높이가 됩니다.
즉 y 좌푯값은 sinθ임을 알 수 있죠.
이렇게 반지름의 길이가 1인 원을
'단위원'이라고 합니다.
cosθ와 sinθ가 곧, 단위원의 둘레를
구성하는 점들의 좌푯값이라고 볼 수 있는 것이죠.
물론 이때 θ( 세타 )를 알아야겠죠.
아래 그림처럼

단위원의 세타( 각도 )가 점점 벌어진다고 합시다.
그럼 세타가 90도가 되는 시점에
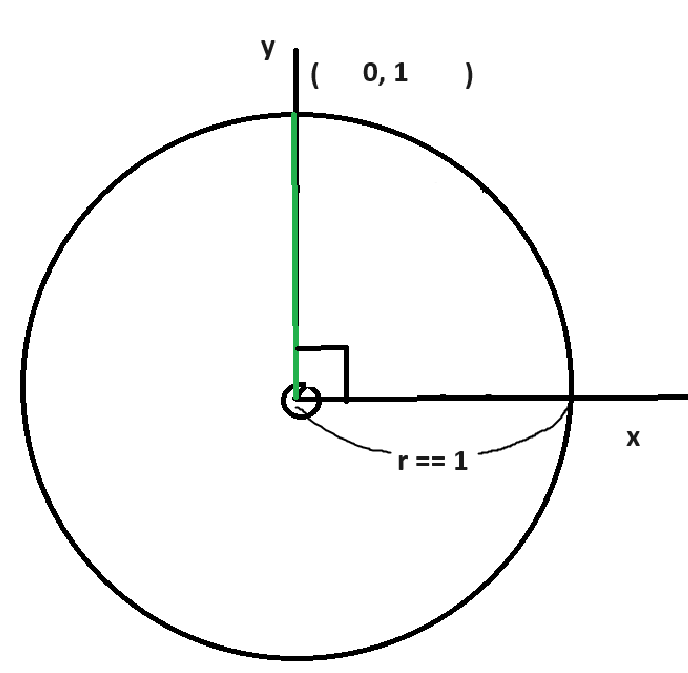
빗변과 높이가 겹쳐지는 순간이 올 겁니다.
이때 단위원에서 x 좌푯값은 cosθ이므로
밑변 / 빗변인데, 빗변이 1고 밑변은
점점 짧아지면서 0으로 수렴하고 있습니다.
이를 대입해 보면 0 / 1,
즉 밑변은 0이 나오므로
x 좌푯값은 0입니다.
단위원에서 y 좌푯값은 sinθ이므로
높이 / 빗변인데 빗변이 1이고
높이는 점점 빗변과 가까워지면서
1로 수렴하고 있습니다.
이를 대입해 보면 1 / 1,
즉 높이는 1이 나오므로
y 좌푯값은 1입니다.
그래프로 표현을 하면
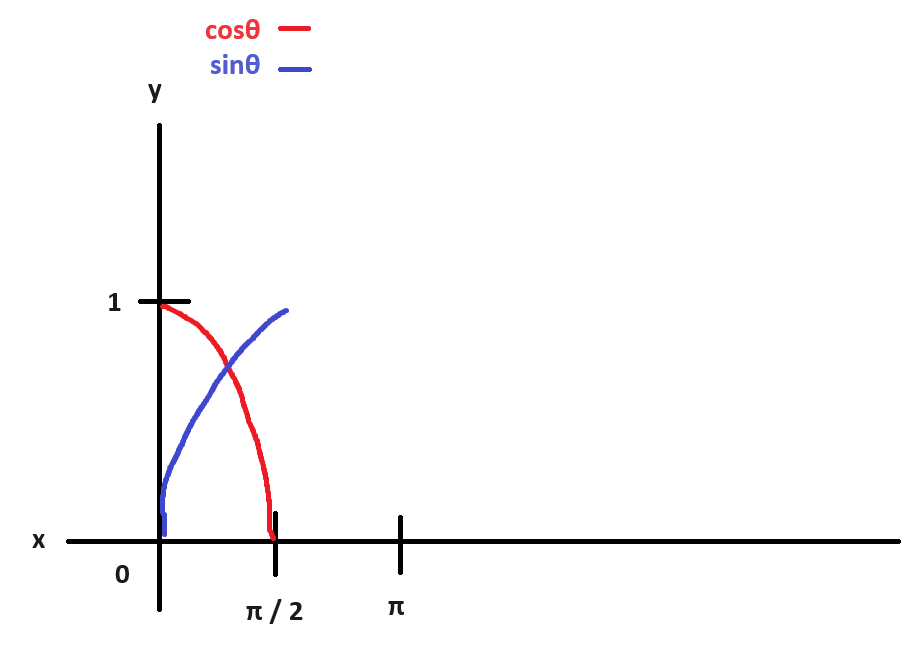
세타가 π / 2, 즉 세타가 90도로 갈수
cosθ가 점점 0을 향해서, sinθ는 점점 1을
향해 가는 것이죠.
세타가 더 커지면서 90도를 넘어가면

직각삼각형이 반대로 구성이 되겠죠.
이 상태에서 점점 세타가 π, 즉 180도로 갈수록
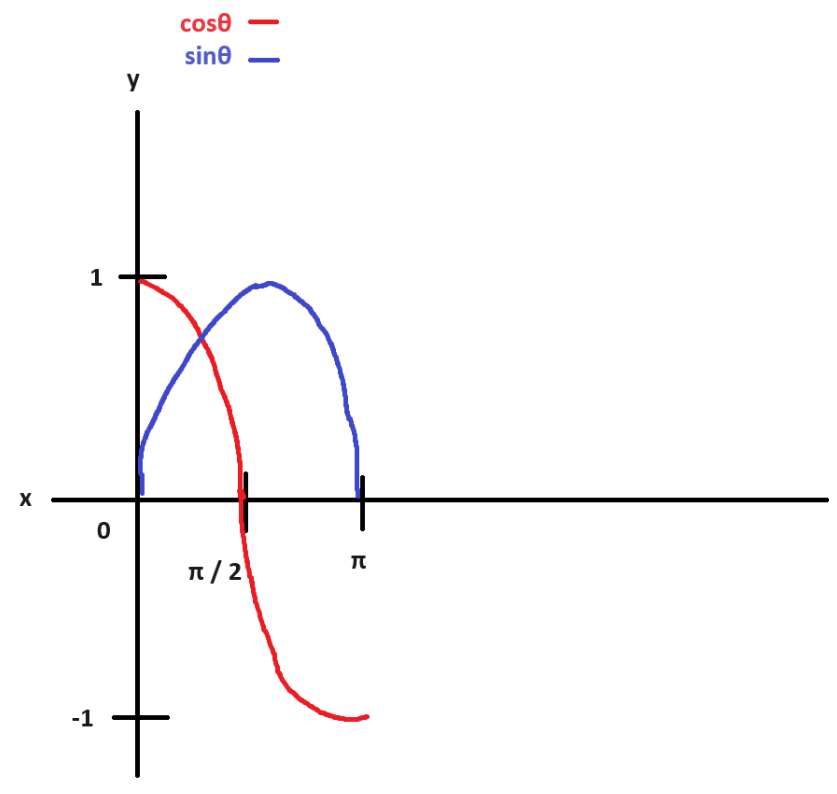
직각삼각형의 x 좌푯값에 해당하는 cosθ는 -1을 향하고
y 좌푯값에 해당하는 sinθ는 0을 향하게 될 겁니다.
그러다가 세타가 180도를 넘으면

직각삼각형이 뒤집히면서 형성되겠죠.
이때 180도에서 -1이었던 x 좌푯값은
세타가 180도를 넘어, 270도에 가까워지면
점점 0으로, y 좌푯값은 0에서
점점 -1로 가게 되겠죠.
그래프로 나타내면
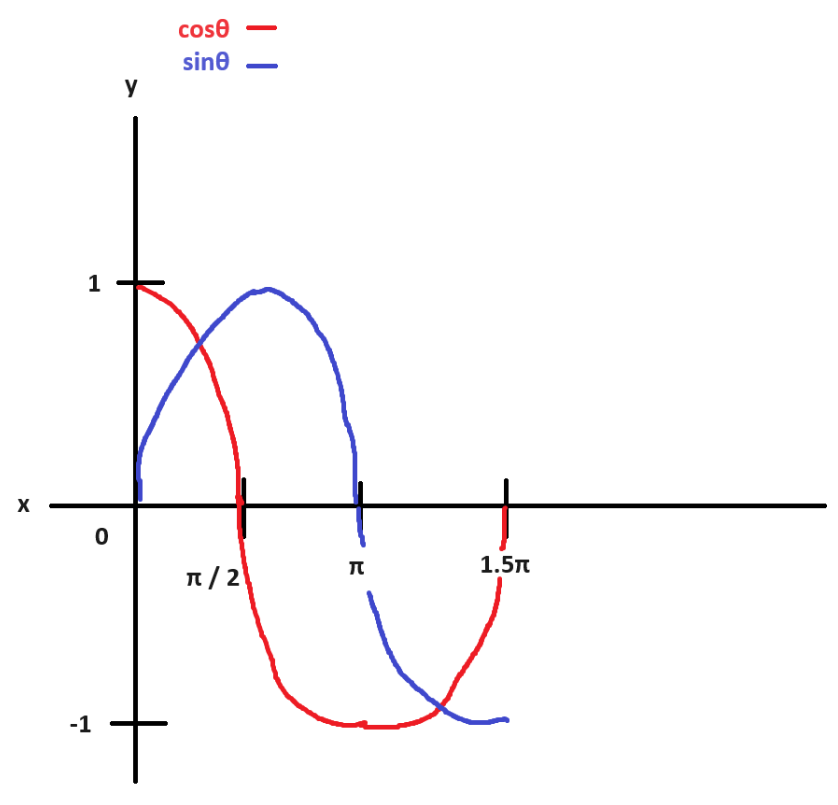
위 그림처럼 진행되는 것입니다.
세타가 270도에서 360도를 향해,
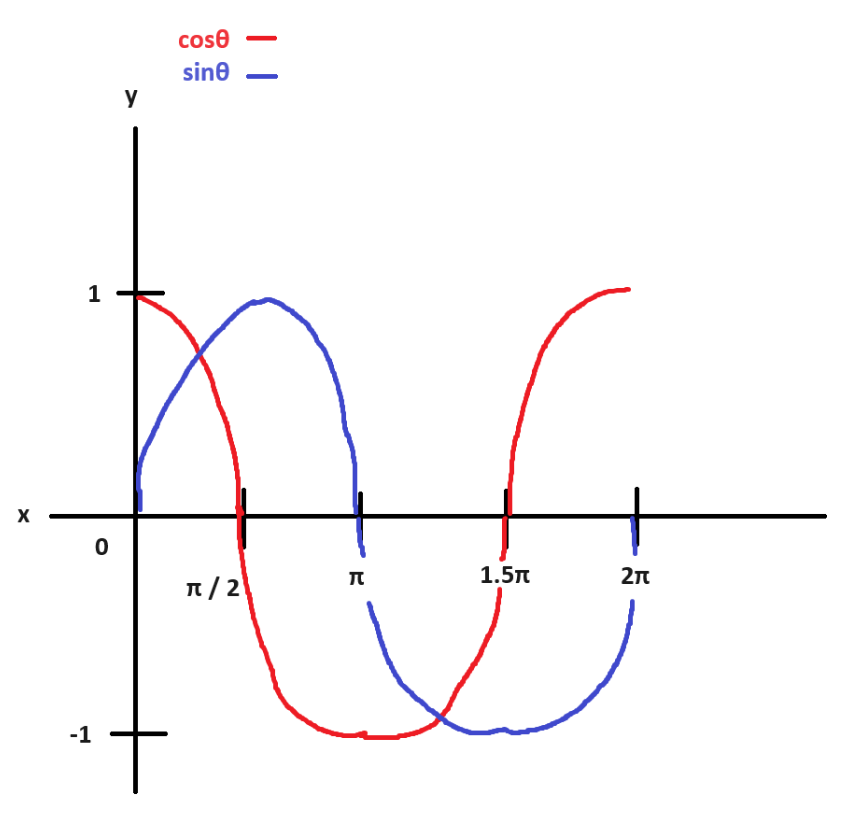
즉 다시 원점으로 돌아오면서
cosθ과 sinθ는 위 그래프처럼
각각 1과 0을 향하겠죠.
이후 세타가 360도를 넘어가면,
다시 처음 상태로 돌아가 위 그래프가
그려졌던 과정을 다시 반복할 겁니다.
위 내용을 토대로 플레이어가
발사할 발사체의 움직임을 구현을 해 보겠습니다.
1초 동안 600의 거리를 이동하는 발사체를
우측 45도 방향으로 발사하고 싶습니다.
단순하게 생각하면 1초 동안 x축으로 600만큼,
y축으로 600만큼 이동하면 되겠다는 생각이 듭니다.
하지만 이렇게 코드를 작성하는 경우,

의도한 600이라는 거리보다 더 멀리 가게 됩니다.
더 멀리 가게 된다는 것을
피타고라스 정리를 통해 알 수 있는데,
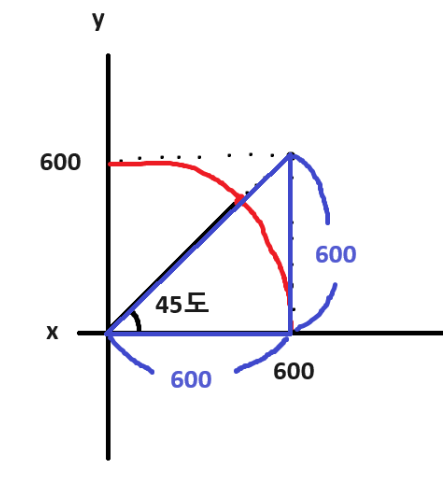
( 600, 600 ) 지점의 점들을 통해
밑변과 높이가 600인 직각삼각형이 형성됩니다.
직각삼각형이면서 각도가 45도이므로
피타고라스 정리 ( 밑변^2 + 높이^2 = 빗변^2 )에
대입해 보면
600^2 + 600^2 = 빗변^2 이고,
720000 = 빗변^2 이므로
√720000 = 빗변 입니다.
√720000은 약 848.52 정도로
위 직각삼각형의 빗변의 길이는
우리가 도달하려는 목표 지점인
600을 한참 넣은 수치입니다.
정말 45도 방향으로 1초 동안 600의 거리를
이동하는 발사체를 구현하고 싶다면
x 좌표가 600인 지점과 y 좌푯가 600인 지점이
서로 호를 이루고 발사체의 방향과
맞닿는 부분을 발사된 지 1초가 지났을 때의
도착 지점으로 해야 합니다.
즉 길이가 600인 직선을 x축으로부터
45도 세운 지점을 도착 지점으로 해야 하는 거죠.
발사체가 45도의 각도로
600의 거리를 이동하게 할 겁니다.
즉 반지름이 600인 원이며
세타가 45도인 것이죠.
반지름이 1인 단위원은
세타가 45도일 경우
x 좌푯값은 cos45도,
y 좌푯값은 sin45도입니다.
단위원과 반지름이 600인 원
내부의 형성되는 직각삼각형은
세타가 45로 동일하므로
'닮음'이 됩니다.
즉 단위원 내부에 형성된
직각삼각형의 빗변, 밑변, 높이의
길이를 600배 해 주면
반지름이 600인 원 내부에
형성되는 직각삼각형의
빗변, 밑변, 높이의 길이를
구할 수 있는 것이죠.
반지름( 빗변 )이 600인 원 내부에
형성되는 직각삼각형의
밑변의 길이( x 좌푯값 )는
600 * cos45도,
높이의 길이( y 좌푯값 )는
600 * sin45도입니다.
CMissile 클래스의 헤더 파일로 가서
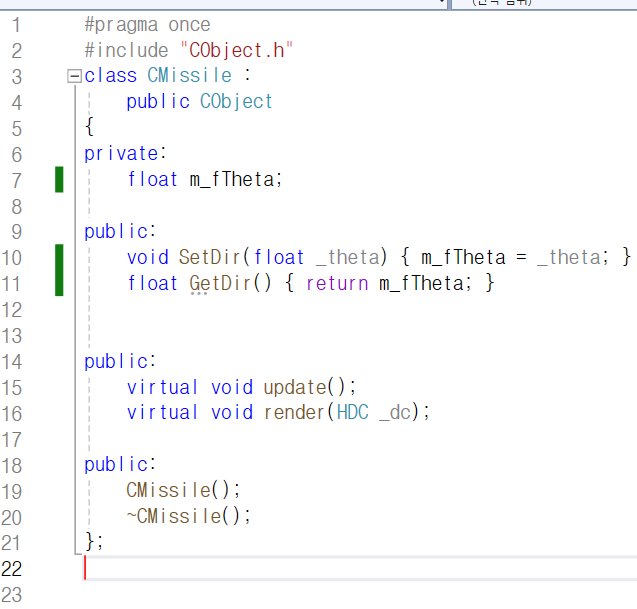
방향을 나타내던 기존 멤버를 수정하여
각도를 나타내는 멤버 m_fTheta로 바꾸어 주겠습니다.
true, false를 통해 방향을 설정해 주던
SetDir 함수도 인자로 받은 값을
각도로 설정해 주는 함수로 바꾸었습니다.
m_fTheta의 값이 0일 때,

즉 발사체가 날아가는 각도가 0일 때
발사체는 어디로 날아갈까요?
아래 그래프를 보시죠.

빗변이 600이고 세타가 0이면
x 좌푯값은 600 * cos0으로
600 * 1 = 600입니다.
y 좌푯값은 600 * sin0으로
600 * 0 = 0입니다.
이 두 좌푯값에 각각 fDT를
곱하였으니 발사체는
초당 x 좌표로 600만큼,
y 좌표로는 이동하지 않겠네요.
실행해 보니 가운데 존재하는 플레이어의

발사체가 정말 x 좌표로만
이동하는 모습을 확인할 수 있습니다.
발사체를 45도 방향으로 이동시키려면
m_fTheta의 값을 45도로 설정해 주면 되겠죠?

M_PI는
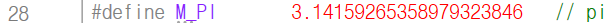
파이를 나타내는 상수로,
전처리기 지시문을 이용해

위 두 코드를 입력하면 사용할 수 있습니다.
π는 라디안에서 180도를 의미하죠?
π / 2는 90도입니다.
그럼 45도는 π / 4겠죠.
m_fTheta의 값을 M_PI / 4.f로 초기화하고
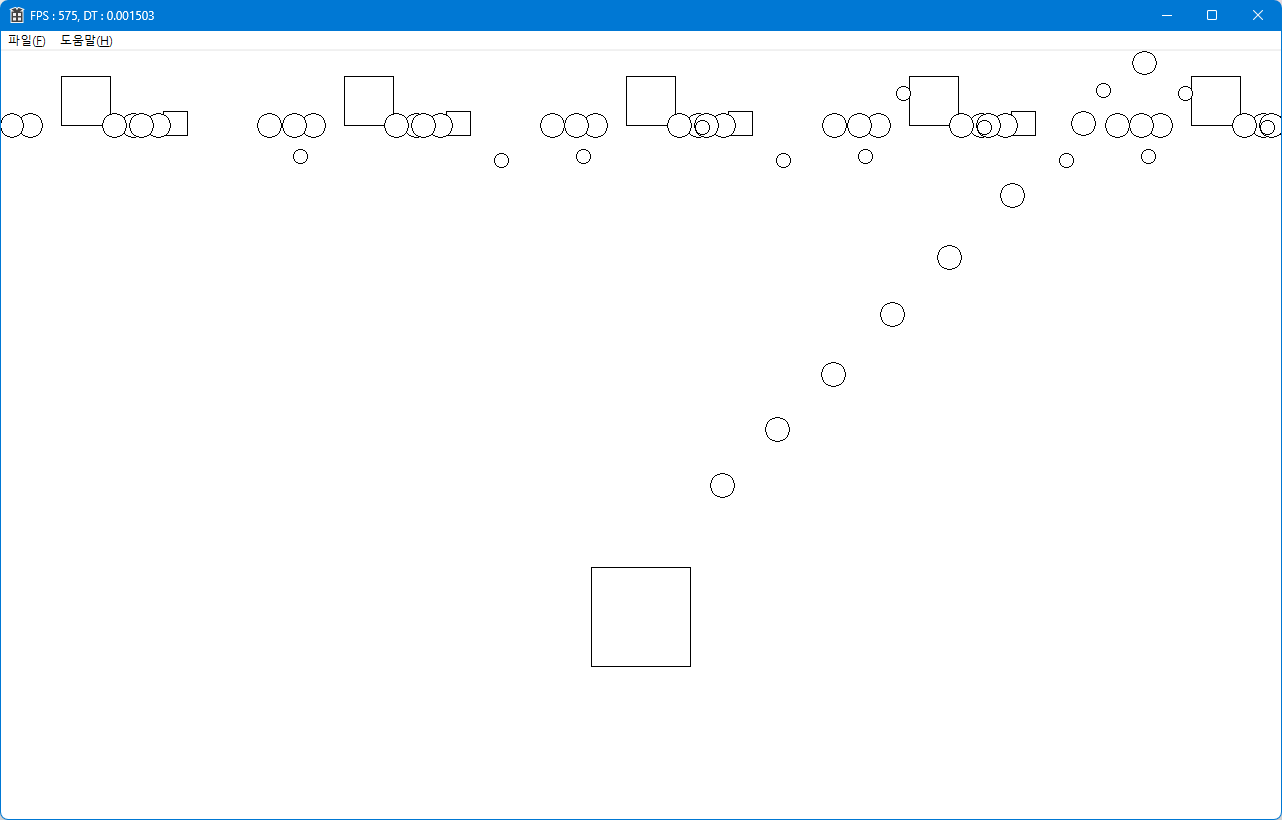
프로그램을 실행하여 스페이스 바를 입력하였더니
정말 45도 방향으로 발사체가 이동하는 것을 확인할 수 있습니다.
만약 플레이어 오브젝트를 기준,
뒤쪽 방향으로 발사체를 날리고 싶다면
m_fTheta를 270도로 설정해 주면 되겠죠.
π / 2가 90도이고 여기에 3을 곱하면
270도가 나올 겁니다.
m_fTheta를

위처럼 초기화해 주고,
프로그램을 실행한 후 스페이스 바를 눌러
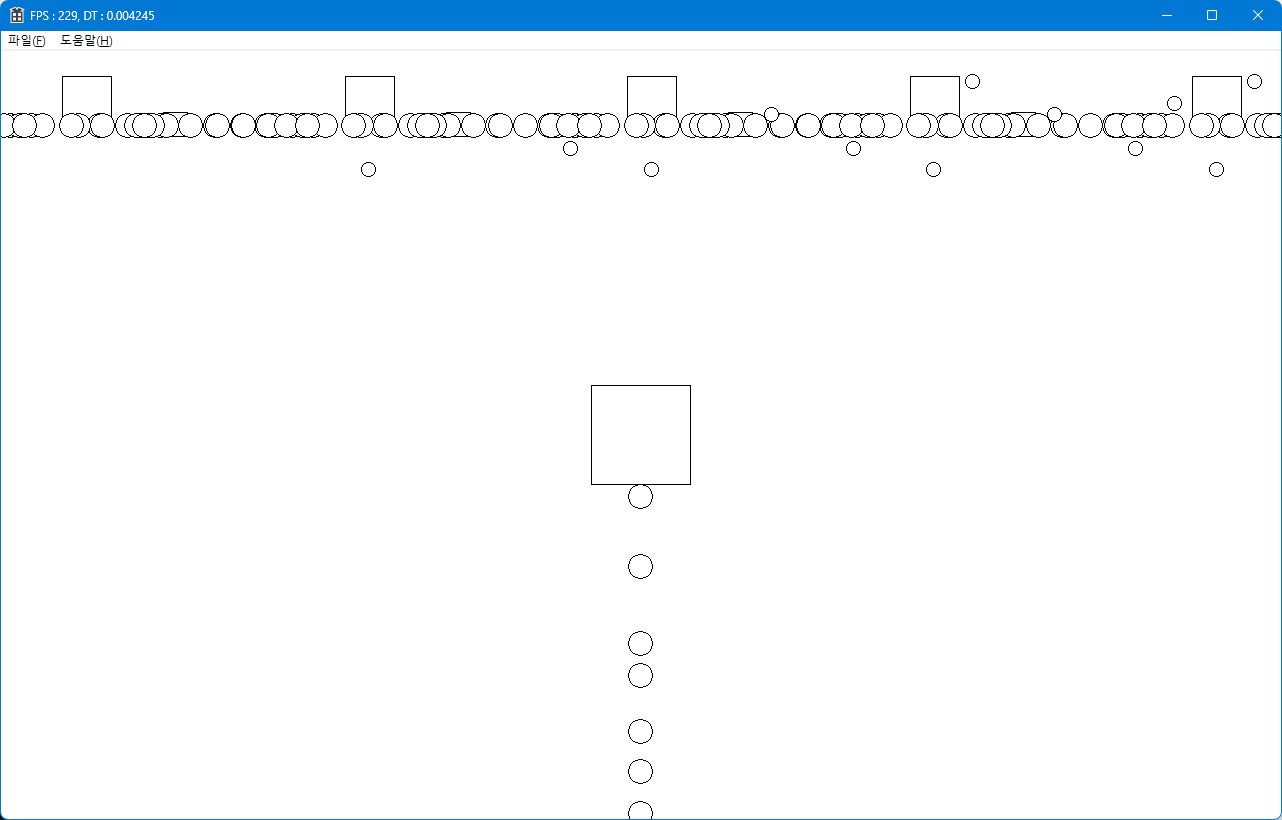
발사체를 발사하면 오브젝트 기준,
뒤쪽으로 발사체가 나가는 것을 확인할 수 있습니다.
강의 출처 : https://www.youtube.com/watch?v=SG4GUVmIEZU
'Win32 API > 기초' 카테고리의 다른 글
| Win32 API 기초 : Resource (1) (0) | 2024.07.13 |
|---|---|
| Win32 API 기초 : 기초 수학 (2) (0) | 2024.07.10 |
| Win32 API 기초 : Object (2) (0) | 2024.07.08 |
| Win32 API 기초 : Win32API Object (1) (0) | 2024.07.06 |
| Win32 API 기초 : Scene Manager (2) (0) | 2024.07.05 |



