Win32 API 기초 : Collider (6)
두 오브젝트의 Collider가
충돌했다는 판정을 어떻게 할 수 있을까요?
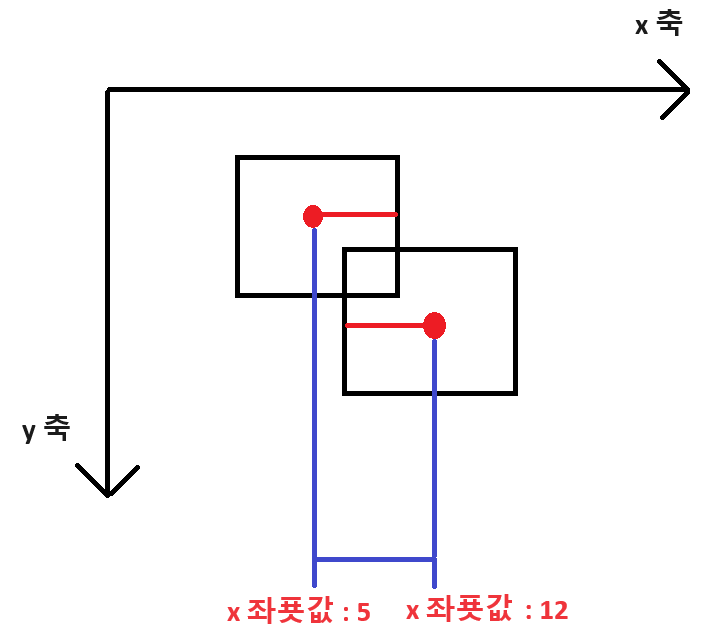
위 그림과 같이 두 Collider가 충돌하고 있는
상황이라고 가정해 봅시다.
왼쪽 Collider의 가로의 총 길이는 10,
오른쪽 Collider의 가로의 총 길이도 10이라고 하죠.
각 Collider의 총 가로 길이를 절반으로 나누고
더하면 10이 나오죠?
여기서 각 Collider의 x 좌푯값을 뺀 값이
10보다 작다면 두 Collider는 충돌하고 있다고
볼 수 있다는 것이죠. 물론 y 좌푯값도
같은 조건을 충족해야 정말 충돌하고 있다고
확정 지을 수 있겠죠.
아래 그림처럼

두 Collider의 x 좌푯값을 서로 뺐을 때
10 이상이라면 충돌하고 있지 않은 것입니다.
이러한 조건 체크를 콜리전 매니저의 멤버 함수인

IsCollision 함수에서 진행하여 두 오브젝트에
존재하는 Collider가 충돌하고 있는지 충돌하고 있지 않은지
판단하는 겁니다.
두 Collider의 좌푯값과 크깃값을 Get 함수를 통해
얻어서 지역 변수에 저장합니다.
114번째 줄에 있는 if 문을 통해
두 Collider의 x 좌푯값을 서로 뺀 값이
두 Collider의 x 축 크깃값을 반으로 나눈 뒤 서로 더한 값보다
작고, y 축 기준으로도 같은 조건을 충족한다면
충돌한 상태로 보고 true를 반환합니다.
해당 if 문에 걸리지 않았다면
충돌 조건을 충족하지 않은 것이므로
false를 반환합니다.
이때 _refRightCollider가 가리키는 Collider가
더 왼쪽에 위치할 수도 있죠. 이 경우 두 Collider의
x 좌푯값에 대한 뺄셈을 진행하면 음수가 나옵니다.
뺄셈을 진행하여 알고 싶은 건 두 Collider가
얼마만큼 떨어져 있는지 알기 위한 것이므로
음수가 나오지 않도록 abs 함수를 통해 뺄셈의
결과를 절댓값으로 바꾸어 줍니다.
Collider 클래스에 int형 멤버 m_IsCol을 추가해

Collider가 현재 충돌 중인지 아닌지
나타낼 수 있도록 합니다.
다른 Collider와 충돌이 시작되면
OnCollisionEnter 함수가 호출되죠?
이때 m_IsCol의 값을 하나 올립니다.
계속 충돌 중이라면 OnCollision 함수가 호출되죠?
이때는 이미 m_IsCol의 값이 하나 오른 상태이므로
그대로 두어도 되죠.
이후 충돌했던 Collider와 떨어지면
OnCollisionExit 함수가 호출되고
m_IsCol의 값이 하나 내려가
해당 Collider와의 충돌에서
벗어났음을 나타냅니다.
차라리 m_IsCol를 bool형으로
선언하여 충돌이 시작되면 true를,
충돌에서 벗어나면 false를 저장할 수도 있으나
이러면 문제가 하나 발생할 수 있습니다.
플레이어가 몬스터1과 충돌한 상태입니다.
플레이어 Collider의 멤버 m_IsCol에는
true가 저장되죠.
계속 충돌을 하고 있는 상태에서 몬스터2랑도
충돌이 발생했습니다. 여전히 m_IsCol는
true인 상태겠죠.
이후 몬스터2가 죽으면서 몬스터2와의 충돌에서
벗어났습니다. 그러면 플레이어 Collider의
멤버 m_IsCol에 false가 저장되겠죠?
하지만 아직 플레이어는 몬스터1과 충돌 중인 상태입니다.
이처럼 단순히 true와 false로 충돌 상태를 구분한다면
여러 Collider와의 충돌 상태를 보존할 수 없기 때문에
int형으로 선언하여 0이 아니라면 다른 Collider와
충돌 중인 상태임을 나타내는 것이죠.
Collider의 최종 위치를 결정하는 finalupdate 함수에서
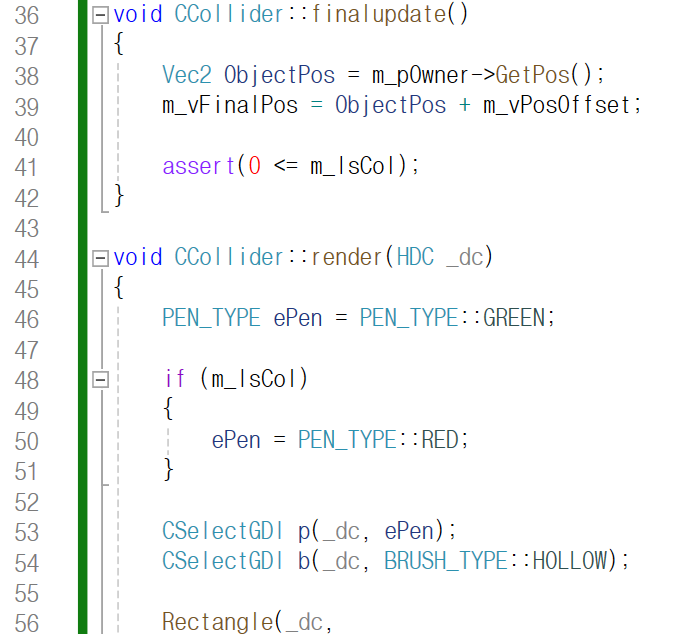
혹시나 멤버 m_IsCol의 값이 음수가 된다면
assert를 진행하여 프로그램을 중단시키고 있습니다.
render 함수에서는 기본적으로
화면 상에 출력되는 Collider의 색상은
GREEN이지만, 만약 멤버 m_IsCol이
0이 아닌 다른 수, 즉 1개 이상의 Collider와
충돌 중인 상태라면 Collider의 색상을
RED로 출력해 주고 있습니다.
강의 출처 : https://www.youtube.com/watch?v=42B4010Ca1A&list=PL4SIC1d_ab-ZLg4TvAO5R4nqlJTyJXsPK&index=30